5. 牛顿方法
牛顿方法(Newton’s Method, Newton-Raphson Method)可以有效地近似实值函数的根。
5.1. 一维
\[x_{n+1} = \ x_n - \frac{f(x_n)}{f^{\prime}(x_n)}\]
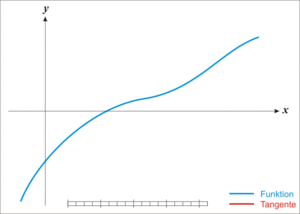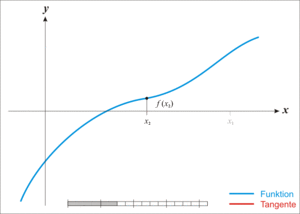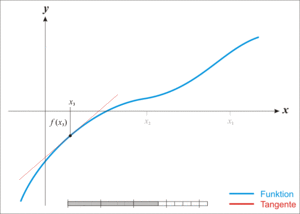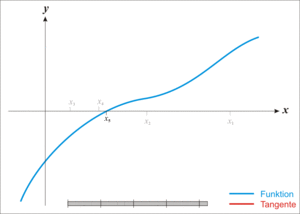
5.2. 高维
\[\begin{split}x_{n+1} &= \ x_n - J^{-1} F(x_n). \\
x & \in \ \mathbb{R}^k,\\
F & : \ \mathbb{R}^k \rightarrow \mathbb{R}^k, \\
J & \in \ \mathbb{R}^{k \times k}, [\text{Jacobian matrix}] \\
J_{ij} &= \ \frac{\partial F_i}{\partial x_j}. \\\end{split}\]
由于求解 Jacobian Matrix 的逆复杂度较高,因此可以通过求解以下等式来节省时间开销:
\[J \cdot (x_{n+1} - x_n) = -F(x_n).\]
5.3. 收敛问题
初始点问题
导数为 0,出现除 0 操作
\[\begin{split}f(x) &=\ 1 - x^2,\\ x_0 &=\ 0, \\ f^{\prime}(x_0) &=\ 0.\end{split}\]死循环
\[\begin{split}f(x) &=\ x^3 - 2x + 2,\\ x_0 &=\ 0, \\ x_1 &=\ 1, x_2 = 0, x_3 = 1, ... .\end{split}\]
根的导数不存在或不连续
有时候收敛速度慢
5.4. 应用
最大/最小化问题
一维
\[x_{n+1} = x_n - \frac{f^{\prime}(x_n)}{f^{\prime\prime}(x_n)}\]高维
\[\begin{split}x_{n+1} &=\ x_n - H^{-1} \nabla F(x_n),\\ H_{ij} &=\ \frac{\partial^2 F}{\partial x_i \ \partial x_j}. [\text{Hessian matrix}]\end{split}\]
求倒数(Reciprocal)
\[\begin{split}f(x) &=\ a - \frac{1}{x},\\ x_{n+1} &=\ x_n - \frac{f(x_n)}{f^{\prime}(x_n)} \\ &=\ x_n (2 - a x_n).\end{split}\]开根号(Sqrt)
\[\begin{split}f(x) &=\ x^2 - a,\\ x_{n+1} &=\ x_n - \frac{f(x_n)}{f^{\prime}(x_n)} \\ &=\ x_n - \frac{x_n^2 - a}{2x_n}.\end{split}\]1def Sqrt(a): 2 x = a 3 while abs(x*x - a) > 1e-3: 4 x = x - (x*x - a) / float(2 * x) 5 return x
1// 向下取整,求整数根:二分法 2int sqrt(int x) 3{ 4 assert(x >= 0); 5 if(x < 2) return x; 6 int left = 0; 7 int right = x; 8 while(left < right-1) 9 { 10 int mid = left + (right - left) / 2; 11 if(mid == x/mid) return mid; // 注意:直接算 mid * mid 会溢出 12 if(mid < x/mid) left = mid; 13 else right = mid; 14 } 15 return left; 16}
5.5. 参考资料
Wikipedia: Newton’s method